このGrasshopperでチェーン構造のバッグをつくるシリーズも中盤です。

だと思います。。 前回メッシュをBrepに変換出来たので、今回は、三角ピースをチェーンで繋げるためのジョイント部分をつくっていきます。

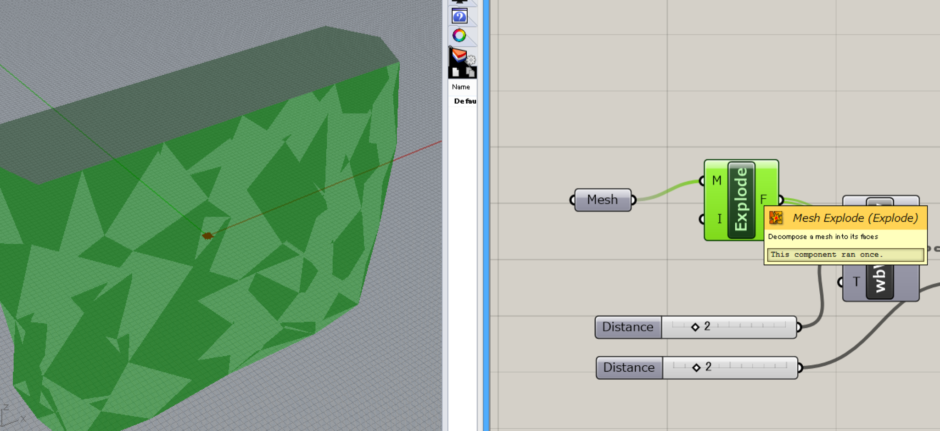
まず、最初の方に作成したMesh Exprodeコンポーネントのところまで戻ります。 このコンポーネントで、ベースとなるメッシュを分解しました。 一つ一つの三角メッシュが格納されている状態です。

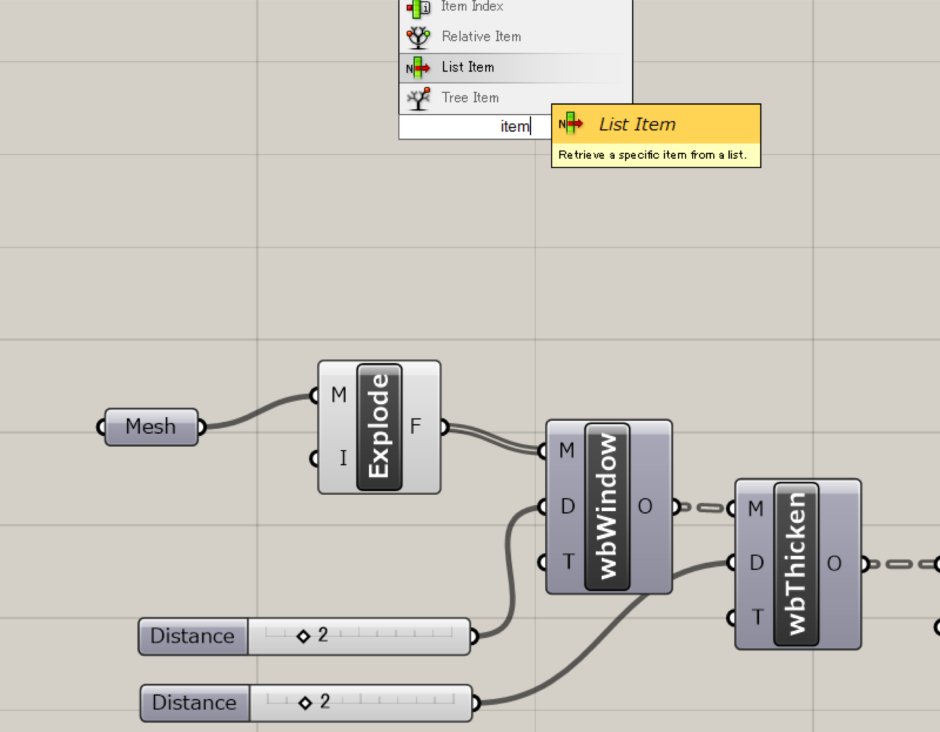
次に、Sets>>List>>List Itemコンポーネントを選択します。

↓図のように接続します。 すると、一つの三角メッシュが現れました。 これは、List Itemコンポーネントのi(Index)にデフォルトで0が入力されているため、0項目のメッシュが抽出されたということです。

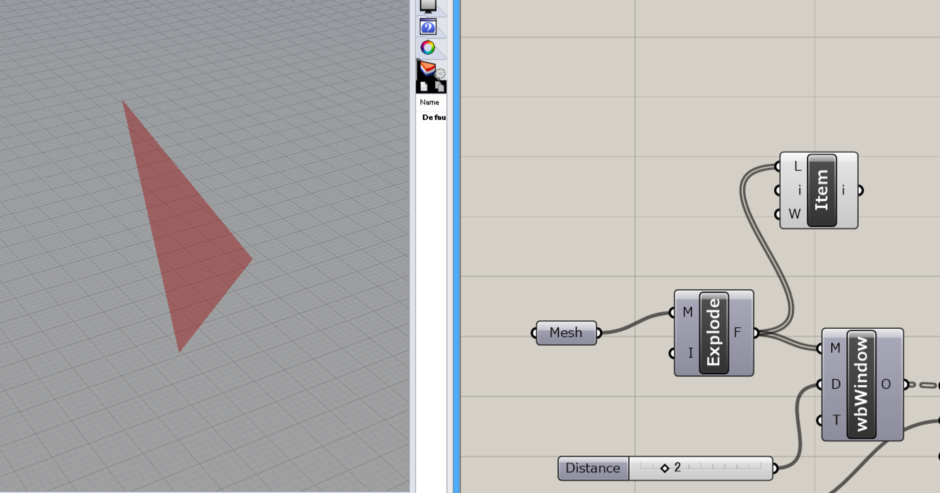
次に、weaverbird’s Face Polylineコンポーネントを選択します。

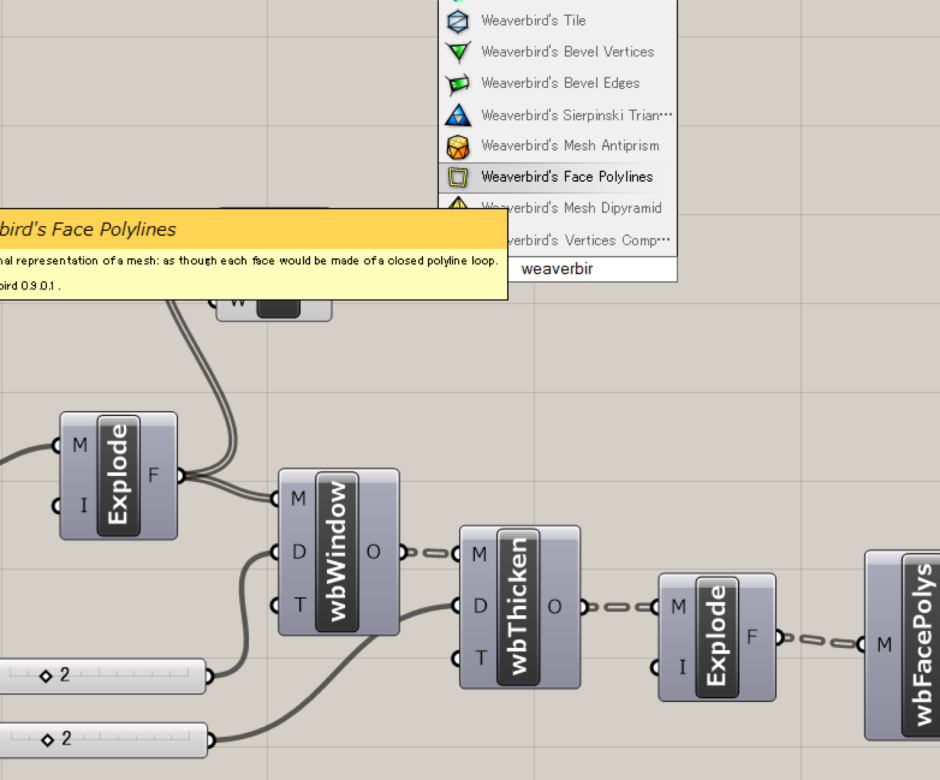
↓図のように接続します。 これで、一つの三角メッシュのアウトラインが取れました。

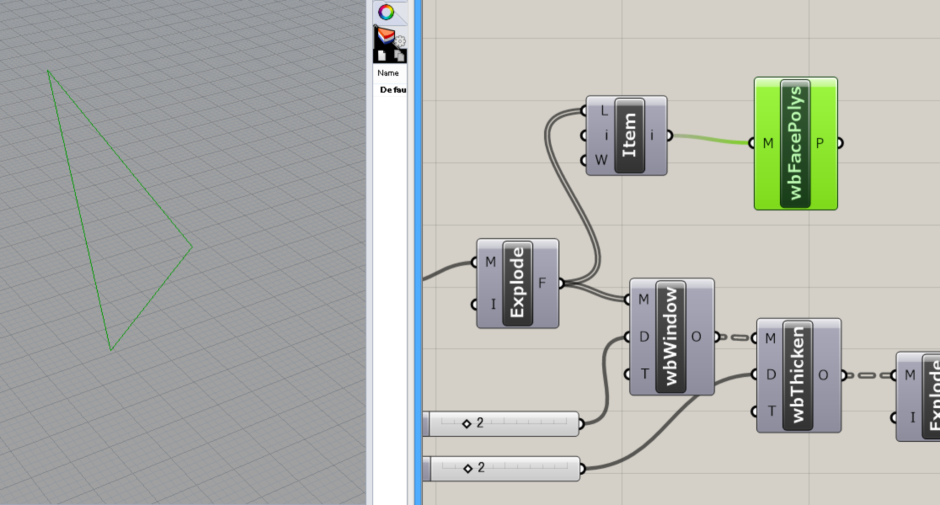
次に、Curve>>Util>>Explodeコンポーネントを選択し、三角形のアウトラインを3本の線に分解します。

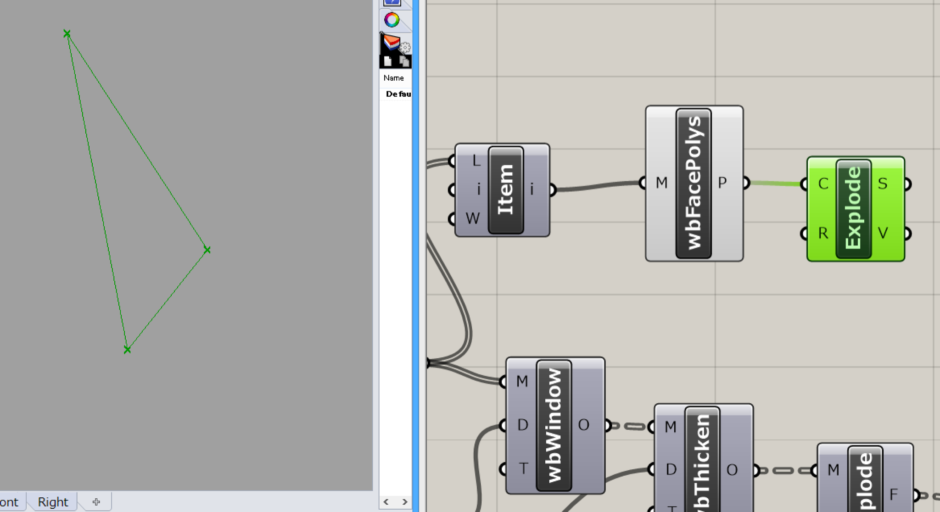
次に、List Itemコンポーネントを3つ複製し、右クリックして、それぞれのi(Index)に0、1、2を入力します。

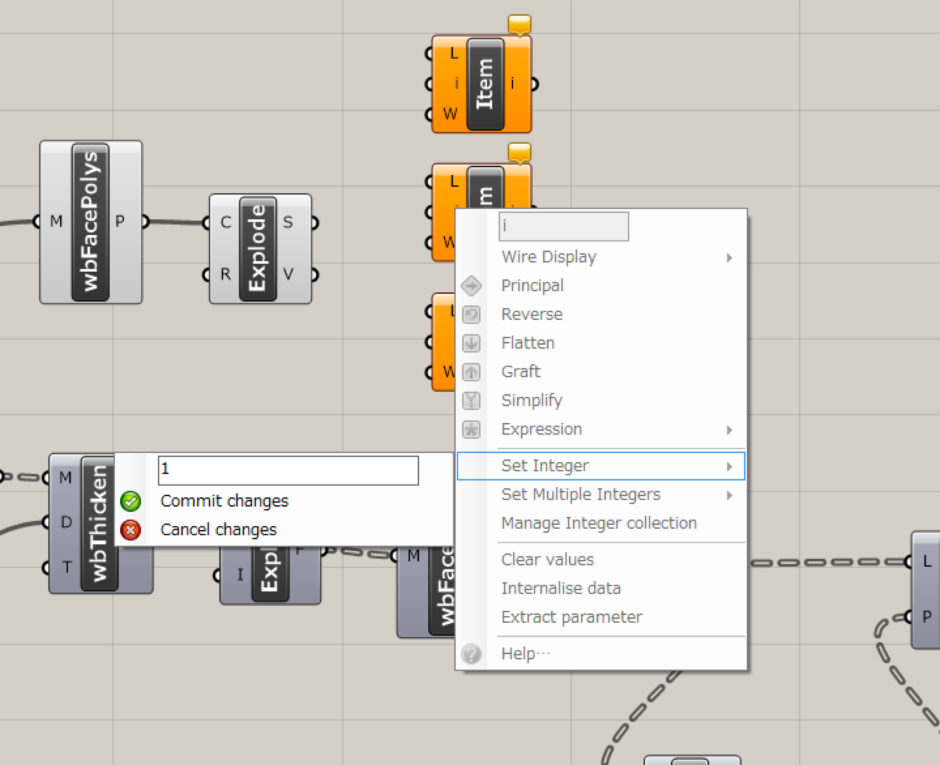
3本の線を1本づつ識別させるためです。

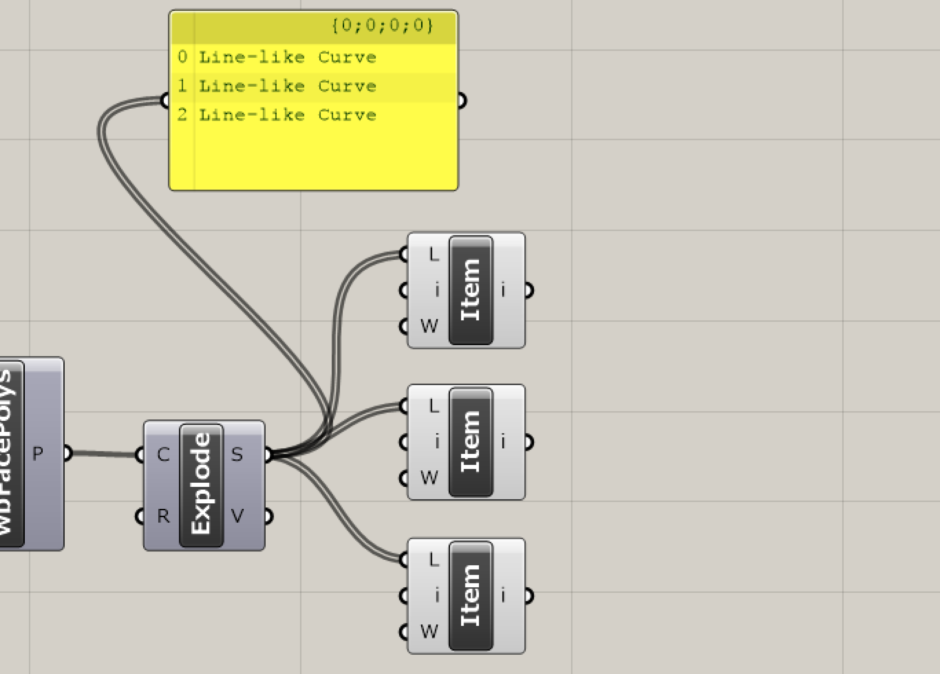
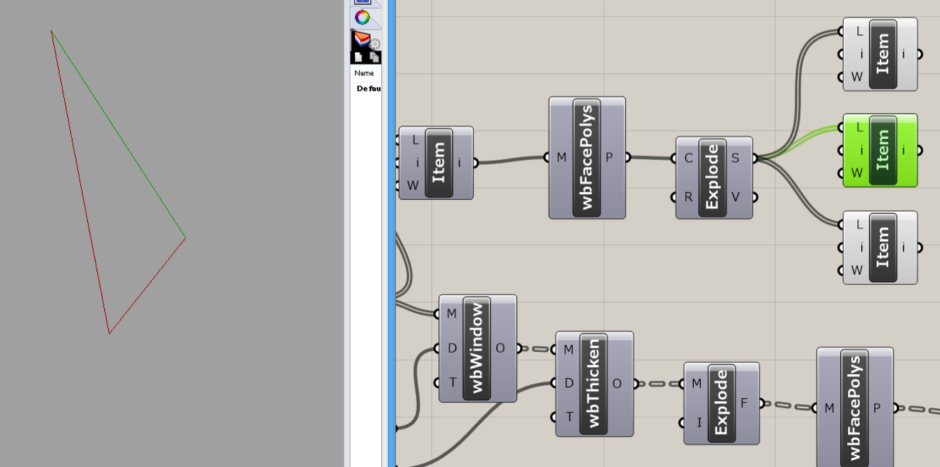
ここから、この3本の線を利用してジョイント等を配置する平面を作っていきます。 ↓図に描くとこんな感じです。

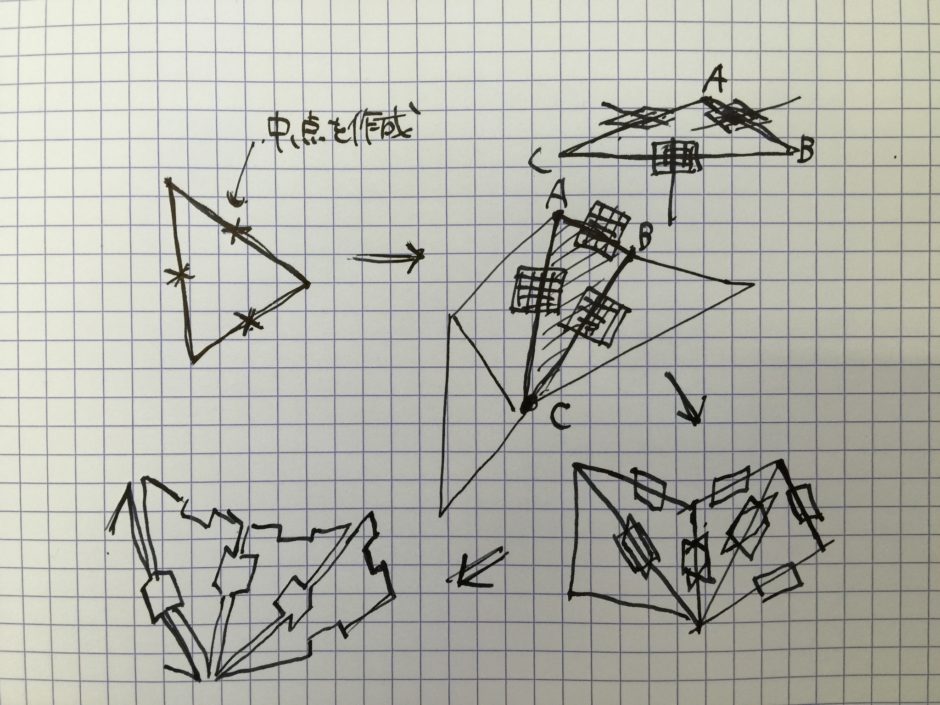
面ABCに平行で、それぞれの線分に対してY軸が垂直に交わる平面を、各線分の中点に配置していきます。 そして、作成した各平面にBrepを置いてブール演算で削ったり、ひっつけたりするといった感じです。

まず、Curve>>Analysis>>Polygon Centerコンポーネントを選択します。

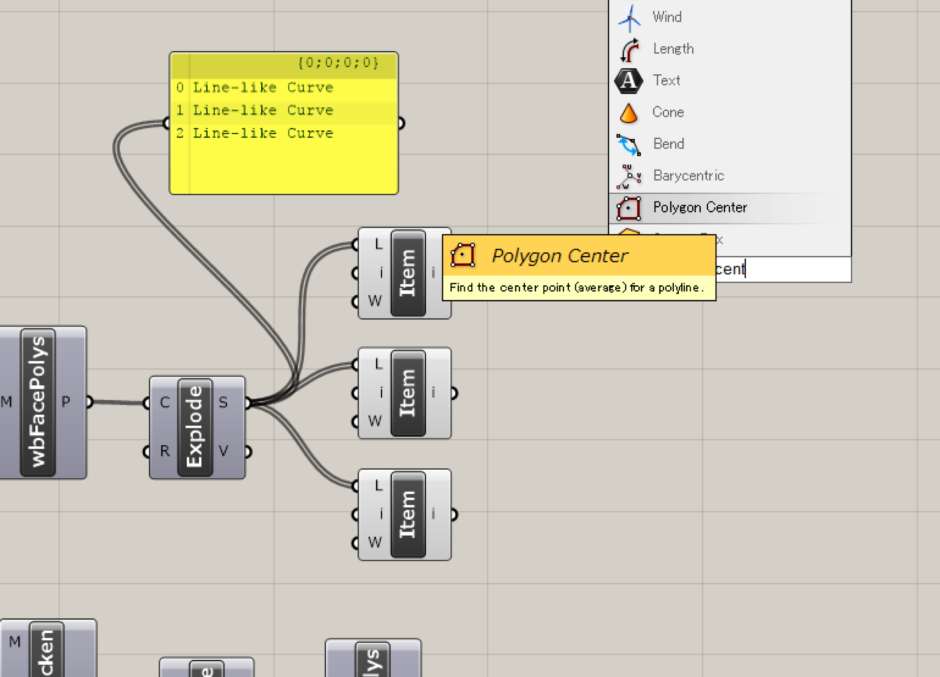
このコンポーネントは、ポリラインの中点を抽出します。

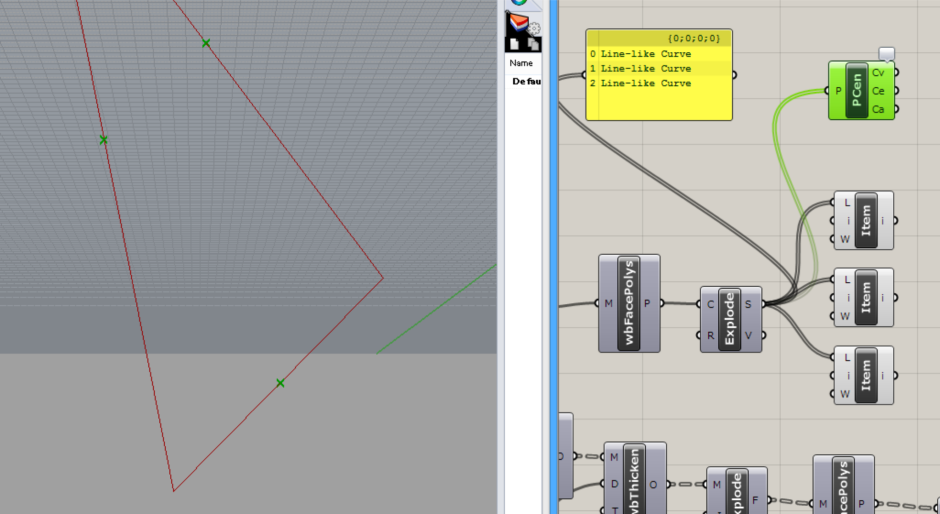
次に、先ほど三角形の各線を識別させるために作ったList Itemコンポーネント3つを複製し、Polygon Centerコンポーネントに接続します。 これで、各中点も識別できるようになりました。

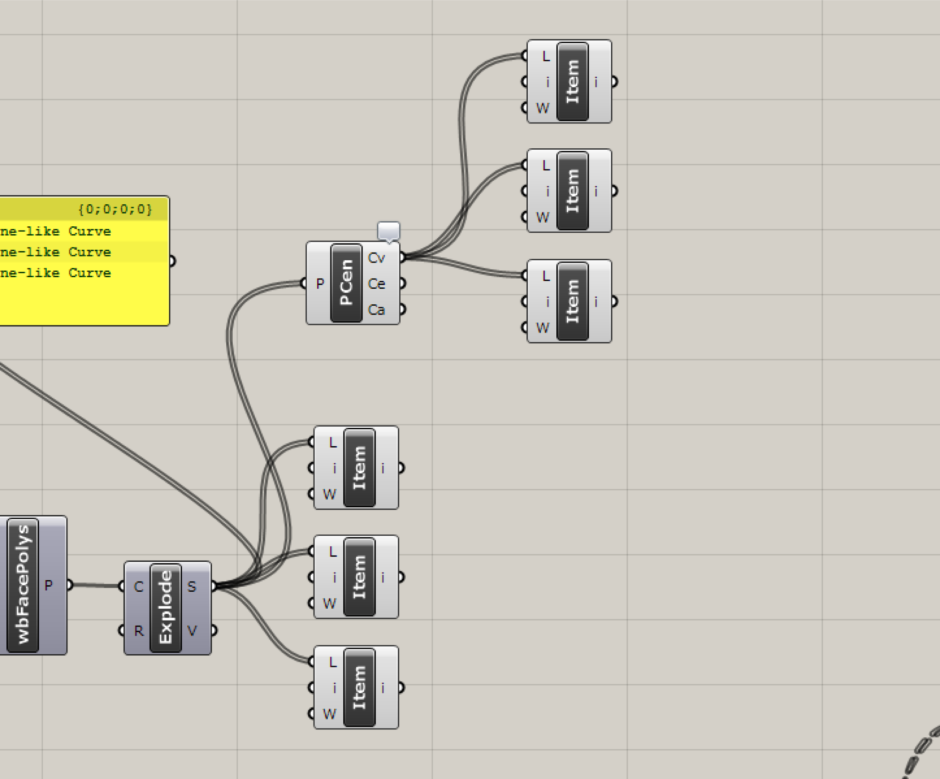
次に、Vector>>Plane>>Construct Planeコンポーネントを選択します。 このコンポーネントは、原点とX、Y軸から平面を出力します。

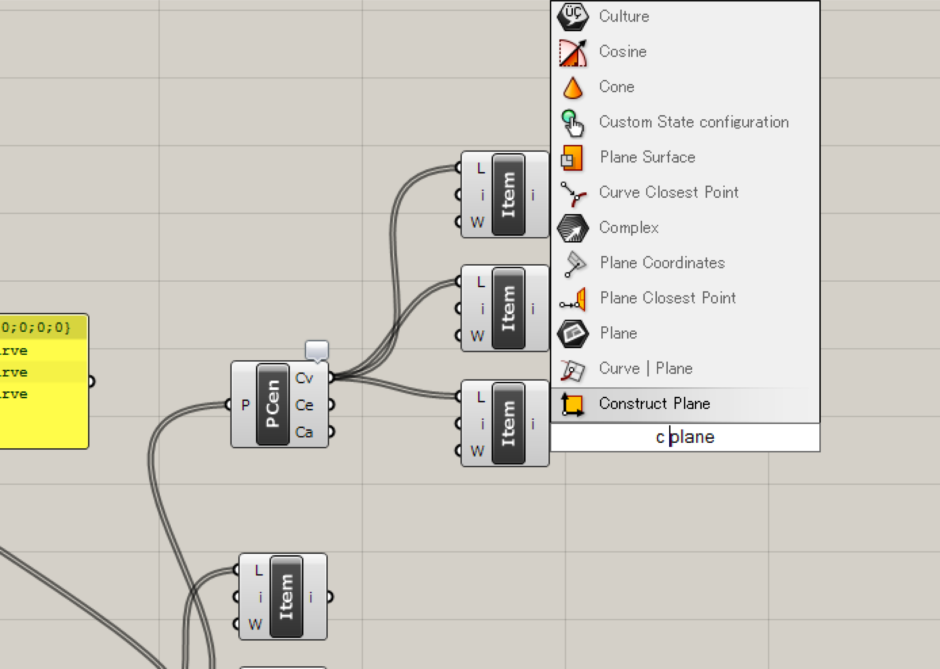
図で描いたように、三角形の面と平行した平面が欲しいので、原点を各線の中点として、任意の2辺をConstruct PlaneコンポーネントのX、Yに割り当てます。 (三角形は任意の2辺がわかれば面が出せるので) ↓図のように接続すると、原点が中点で、線分に対してy軸が垂直に交わる平面が出来ました。

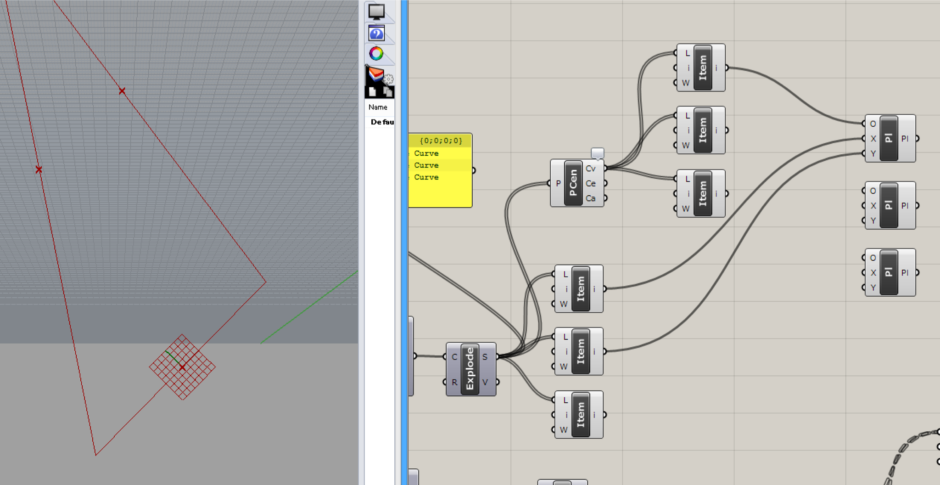
↓図のように接続して、すべての辺に対して平面を出力します。

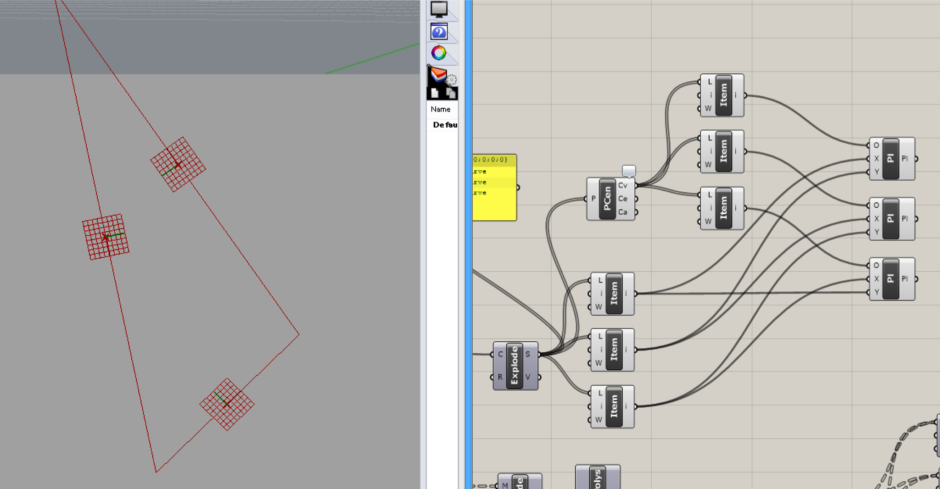
次に、Transform>>Euclidean>>Orientコンポーネントを選択します。

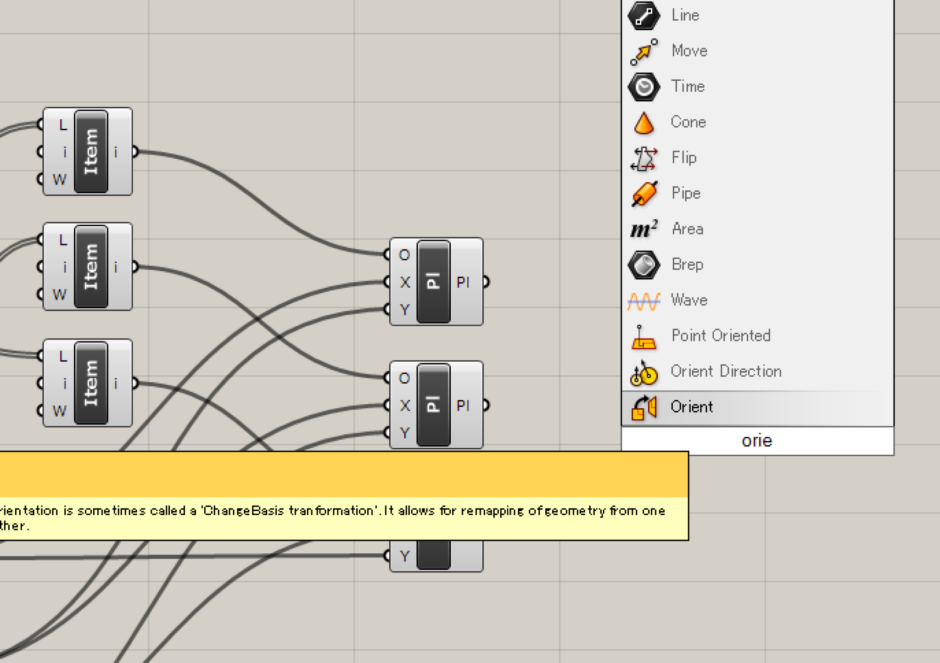
このコンポーネントは、Aのソースとなる平面（デフォルトではワールド平面）にあるGのオブジェクトをBのターゲット平面に配置します。 ↓図のように接続します。 これで、ターゲットが先ほど作成した各平面になります。 Aのソースとなる平面は、デフォルトのままでワールド平面にします。

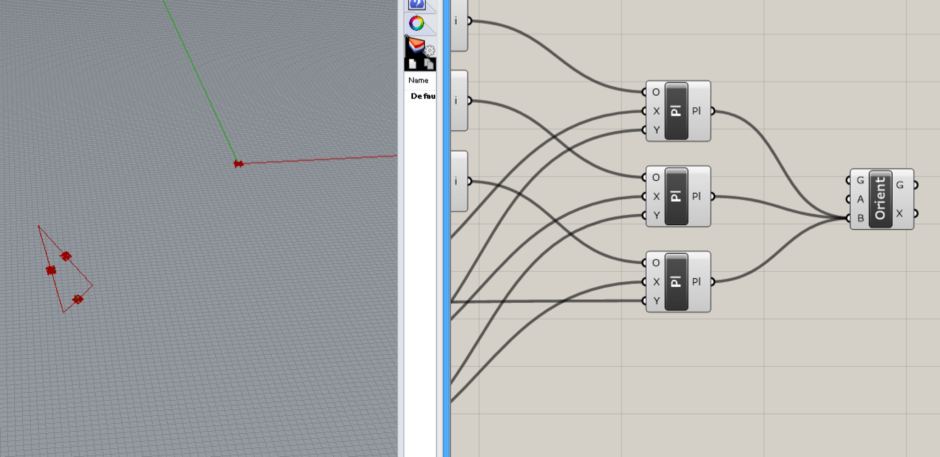
ちょっとテストしてみます。 ワールド平面の原点に図のような立方体を作成してみました。

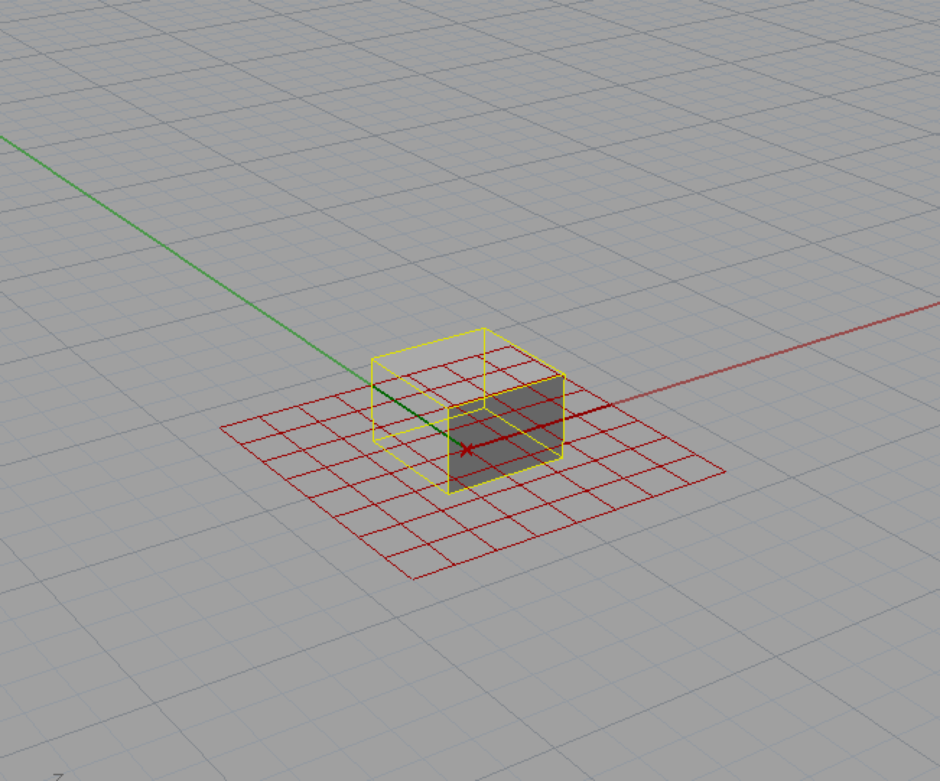
BrepコンポーネントをOrientコンポーネントのGに接続し、右クリックからSet one Brepを選びます。 先ほど作成した立方体を選択します。

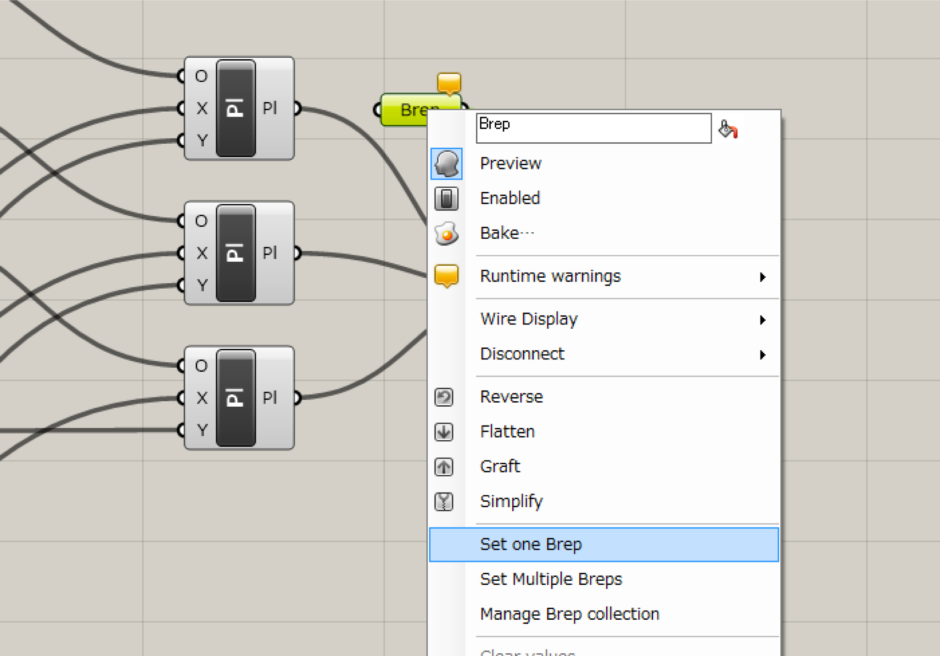
↓問題なく配置されました。

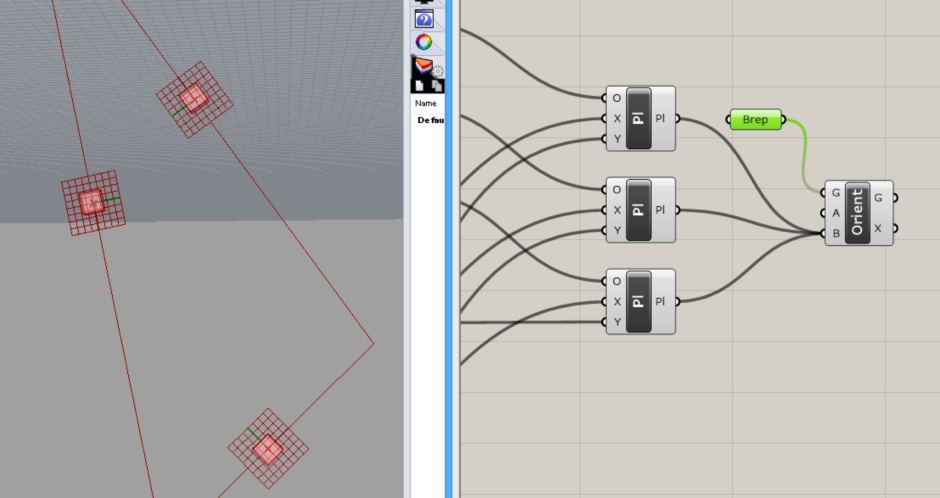
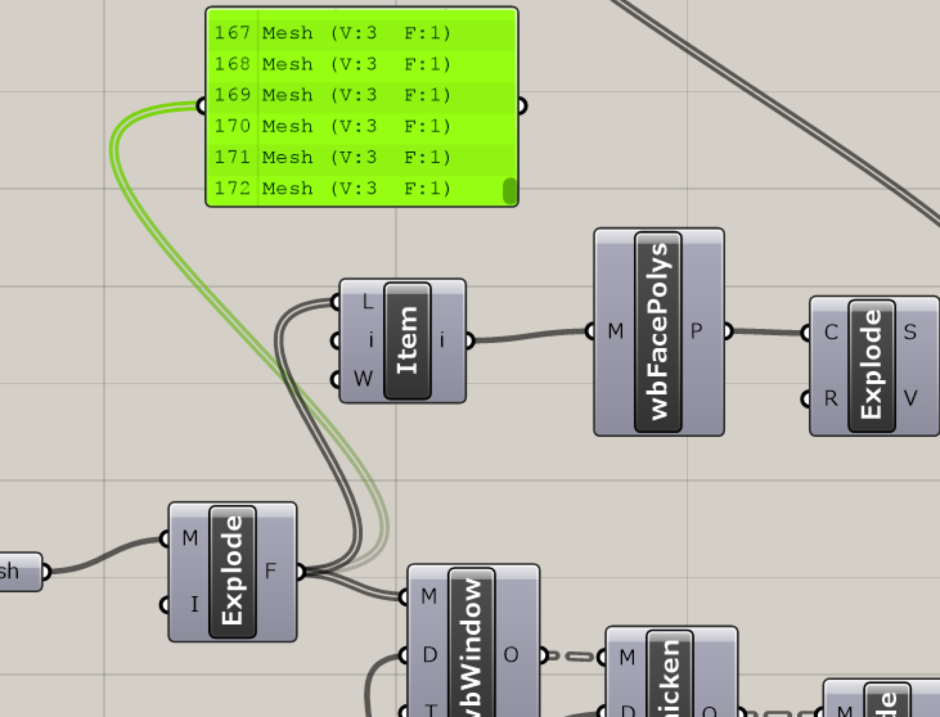
とりあえず一つ出来たので、これをすべての三角メッシュに反映していきます。 最初の方に作ったList Itemコンポーネントまで戻ります。

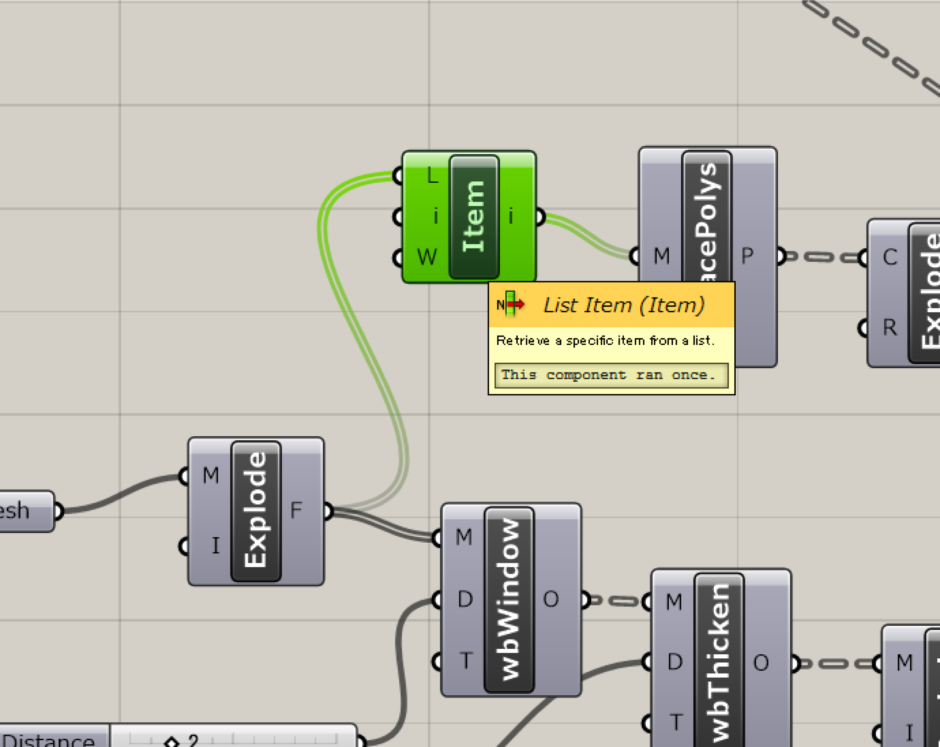
このList Itemコンポーネントは、i(Index)がデフォルトの0のまま使用していたので、出力された三角形が一つでした。 List Itemコンポーネントを右クリックして、Set Multiple Integersを選びます。 複数の数値を入力できるウィンドウが現れるので、こちらに数値を入力していきます。

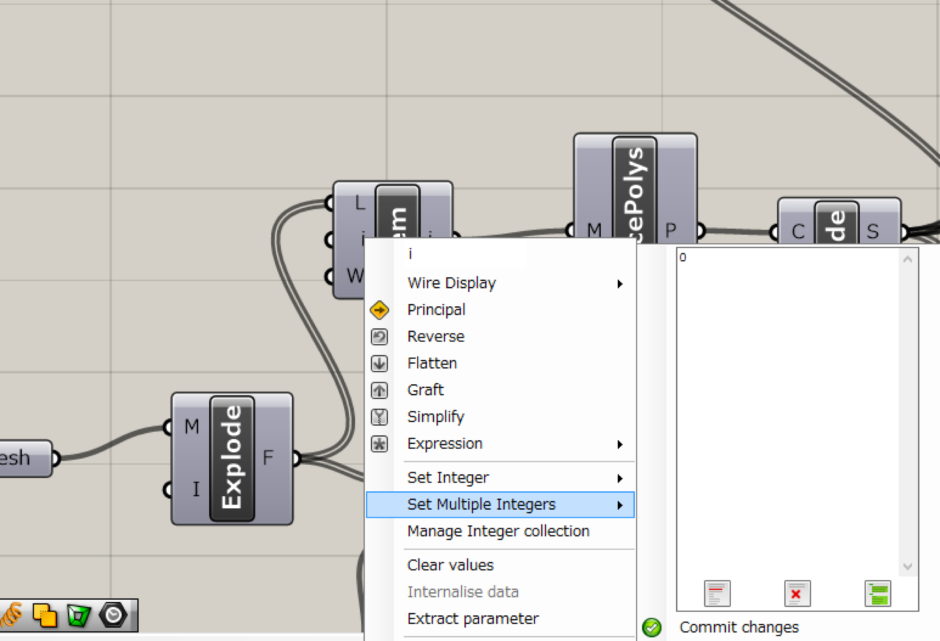
PanelコンポーネントでMesh Exprodeコンポーネントを調べてみると、0〜172項目、合計173個の三角メッシュがありました。

先ほどのSet Multiple Integersに0〜172まで入力します。 （Excelとかで連番作ってペーストすると楽です）

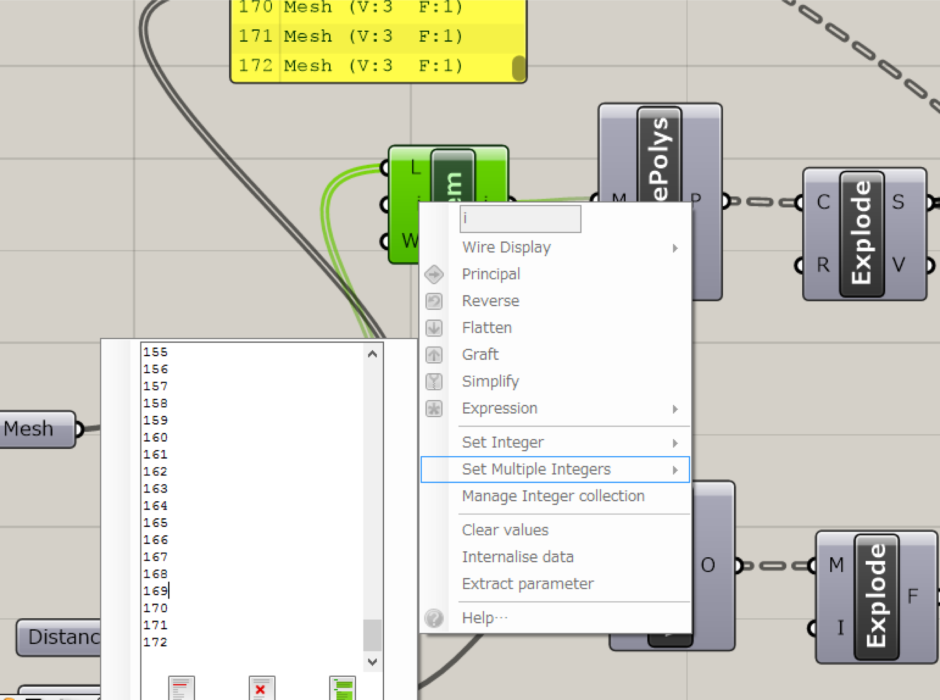
↓こんな感じなりました。

↓立方体を配置するとこんな感じです。

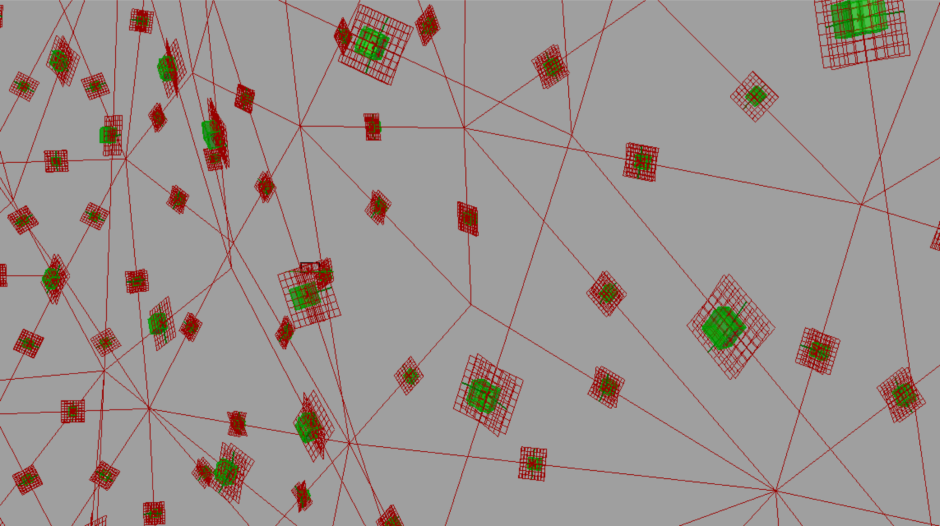
↓とりあえずBakeしてみました。

ベースになる平面が出来たので、これを使って三角ピースのフチを切り取ったり、穴を作ったりなど色々出来るようになりました。 次回は、実際にジョイントパーツを作っていこうと思います。